Pulling force - and other forces
by Flemming Lund, DMJK (first published in Danish in "Signalposten" no. 5, 1975)
After the first trial runs on the new layout at Gb (Copenhagen goods yard) and the inauguration I have been asked if it is possible to predict the pulling performance of a given locomotive. I have for a long time had an interest in the subject; in this article I will try to give an overview of the physical relations that influences pulling performance and a simple set of rules that may be used when construction model locomotives and rolling stock. Evidently such considerations will have to be quite general and therefore must be taken with some reservation; they may, however, be used as guidelines. But let me start on a series of explanations that I hope may be understood by the reader and start with:
1) Prototype weight and model weight
We build our models in 1:45 scale ratio regarding linear measurements, but the weight ratio will for the most part be different. If weight should scale according to the linear scale ratio, 1 ton of prototype weight equal appr. 11 g of model weight in 1:45 scale, as weight reduce in the third power of linear scale ratio as length, width and height are all reduced.
A type A passenger carriage weighs appr. 32 tons, which should equal a model weight of 32 * 11 = 352 g. I think that in average a model of this carriage will weigh appr. the double. If we consider a type MZ diesel locomotive that has drive on all six wheel sets, the prototype weighs appr. 120 tons in operational condition, equal to a model weight of 120 * 11 = 1320 g. If we use the same ratio as for the carriage, the type MZ diesel locomotive would weigh appr. 2600 g. This weight sounds feasible for such a model but in practice the pulling performace may be found lacking.
The explanation is quite straightforward: First it is not that easy to built a model locomotive with six-axle drive so many modellers may use only two or four axle drive. Hence the adhesion weight, i. e. the weight on the driven wheel sets, and also the maximum pulling force will be reduced. Second the layouts are built with heavier grades due to place restrictions, and the curve radii used (often 2m minimum curve radius) are less than allowed by the Danish State Railways in harbour track. The average rolling resistance from a string of wagons is also larger relatively for the models than for the prototype; I will return to this later on. These conditions make it necessary to increase the weight of model locomotives as well as reducing the weight of rolling stock as much as practically possible if we want to run trains of the same length as the prototype.
I will refer to the standards of the Danish Model Railway Club; I recommend that everyone building models in 1:45 scale read them carefully.
"Summary"
Rolling stock is built as light as practically possible.
Locomotives are built with as large adhesion weight as practically possible.
2) Rolling resistances
In order to give any values we shall consider how large forces must be used to move a wagon, or the rolling resistance of a given wagon. Rolling resistance may be divided in three parts:
- Rolling resistance on straight and level track.
- Rolling resistance on straight track on ascending grade.
- Rolling resistance curved and level track.
In practice we must consider the worst case when the three resistance forms are present at the same time as is the case on the new layout at Gb. The conclusive examples reflect this.
To measure rolling resistances I have used an incline as shown in fig. 1; when a wagon is running down the incline with constant speed forces are in equilibrium. The wagon weight P is thought to act in the mass centre of the wagon and is allways acting vertically downward. P is decomposed in two components N and F perpendicular and parallel, respectively, to the rail surfaces on the incline. At constant speed the force F trying to pull the wagon down the incline is equal to but opposite the force F' trying to hold the wagon back, or in other words the forces acting on the wagon are in equilibrium.
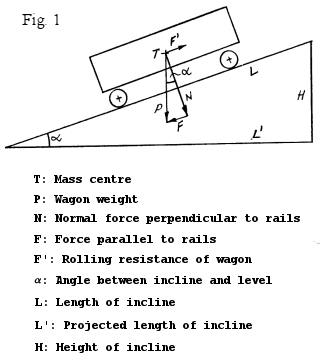
Mathematically F = F' is calculated from:
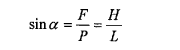
as the triangle PNF is equiangular with the triangle LL'H.
In order to give a general term for the rolling resistance it is calculated in grams per kg of wagon weight and is called Q.
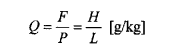
The rolling resistance Q is composed of two parts a) rolling resistance between wheel and rail and b) friction in the bearings. The first can hardly be mea-sured with smooth thread surfaces, while bearing friction has crucial importance so we study this further.
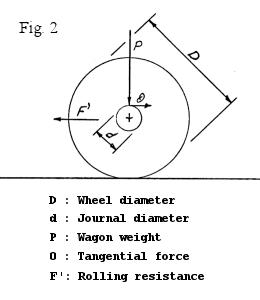
Fig. 2 shows a wheel set with a journal. To find an expression for the resistance the work (force times length) for a given length of travel, here one turn of the wheel set, is calculated.
Using the designations in the figure, as the outer work at the thread shall be equal to the inner work at the journal and the tangential force O = the coefficient of friction µ times the wagon weight P, we get:
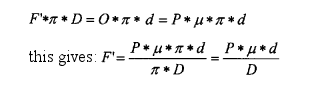
This equation tells that the smaller the wheel diameter D and the larger the journal diameter d the larger the resistance will be. This is confirmed by the tests I have carried out, the factors are shown in fig. 5 and 6. But back to where we started and:
2-1: Rolling resistance on straight and level track
These tests are carried out using wheel sets to DMJK standards sheet 6, which is shown in fig. 3, with 22mm diameter corresponding to 1m prototype wheel diameter. On the standards sheet 6 please notice the 3° thread coning which cause the flanges on straight track not to touch the rail heads, and second, the fillet between the thread and the flange. This has a large impact as I will try to show in the next section.
Click to see >> fig. 3
Here I have to put in an assumption, or assertion if you will, as I will argue that lubrication with thin oil as is often used is of limited advantage; the disadvantages, the posibility of oil on wheels and track, are far greater than the advantages. The oil dries out in the open bearing perhaps as fast as in 2-4 weeks and may leave a sticky residue that increases resistance.
| Bearing type | Resistance in g/kg |
| Brass bearing | 18-22 |
| Brass & Molykote | 15-19 |
| PTFE bushing | 12-16 |
| Ball bearing | 6-10 |
| Wheel diameter in mm | Factor |
| 14 | 1,6 |
| 16 | 1,4 |
| 18 | 1,2 |
| 20 | 1,1 |
| 22 | 1,0 |
| 24 | 0,9 |
| Journal diameter in mm | Factor |
| 1,5 | 0,75 |
| 2,0 | 1,0 |
| 3,0 | 1,5 |
| 4,0 | 2,0 |
| With ball bearings | 1,0 |
For this reason I have carried out all tests except one using non-lubricated bearings. The Molykote grease I have used keeps its properties for a very long time. A set of bearings that I have had running for four years now still has its grease in good condition.
Four types of bearings have been tested:
- normal brass or bronze bearing,
- same as a) lubricated with Molykote Pasta G Rapid,
- bearing with PTFE bushing,
- ball bearing.
The test results are shown in fig. 4; the tests do show quite some variation which is usual when testing. I believe that the test results are representative when there is no jamming of the bearings and no other irrelevant matters influencing results. The resistance values are decreasing with increasing wagon weight but only very little.
Comparing the test results with resistances for prototype railway wagons, the prototype resistance may be as small as 2-3 kg/t or g/kg wagon weight. The difference is probably caused by the more secure bearings and installation and better lubrication of the prototype wagons that we have no possibility of copying in model form.
2-2: Rolling resistance on straight track on ascending grade
To find out about this we once again return to the incline shown in fig. 1. Last time we set the wagon to roll down the incline with constant speed and called the resistance F'; this time we will try to pull the wagon up the incline. To do this we must overcome the wagon's rolling resistance on straight and level track, but furthermore we must overcome the force F parallel to the rail surfaces and hence the wagon weight. It is deduced as before from:

As the angle a is very small I introduce only an insignificant error by setting L = L' and get the more handy expression:
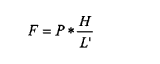
The expression H/L' for L' = 1000 is the same as the grade in promille (per thousand). The resistance that must be added to the resistance on straight and level track is hence in g per kg wagon weight = the grade in promille. If the grade is for instance 10 promille the resistance is 10 g/kg. The largest grade on the new layout at Gb is 16 promille i. e. a resistance of 16 g/kg.
"Summary"
The grade is determined by the layout design so we must accept that the resistance is of this magnitude; we can only influence the wagon weight which should be kept as low as possible.
2-3: Rolling resistance curved and level track
I have not managed to deduce curve resistance mathematically but only by trial. I would like to emphasize two things. One is that we most often for space reasons use curves of 2m radius on our layouts, this is equal to 90m at the prototype. This curve radius is in fact less than recommended by the Danish State Railways on harbour and industrial tracks. In short, it looks like express train speeds on harbour track. Second is that in a 2m radius curve a standard wheel set cannot roll on the threads; if the wheels have the fillet between thread and flange shown in the standards sheet 6 (fig. 3) the outer wheel will roll a bit up on this fillet to increase the diameter sufficiently.
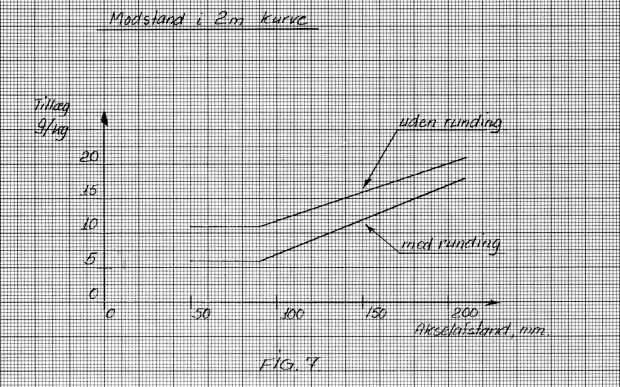
If there is no fillet the wheel will "scrape" its way through the curve. Fig. 7 shows the results from my tests with wheel sets with and without fillet between thread and flange. In the tests there are also some variations in test results so fig. 7 should be taken as a tendency.
The wheel base is the distance between the two outer wheel sets on a rigid-frame wagon. For bogie carriages (cars with trucks) the bogies/trucks are considered as two wagons with short wheel base and hence the bogie/truck wheel base is used in the diagram. The resistance value taken from the diagram is added to the wagon resistance on straight track.
For prototype railways the engineering handbook "Hütte", Volume III, indicates an empirical formula according to Röckl:
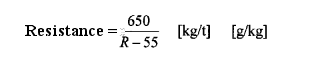
where R = curve radius in m.
R = 90m inserted in this formula gives a resistance of 18.6t/kg or g/kg. It is stated that the result is depending on wheel base but not how. In "Track guidelines" for the Danish State Railways the same formula is used for reducing grade in curves in order to give constant resistance. Considering these informations I would guess that the formula is deduced for a rather long wheel base. In my opinion the test results shown in fig. 7 ought to be larger than is the case compared to Röckl's formula. At this time I cannot explain the difference.
"Summary"
1) Wagon weight should be kept as low as practically possible.
2) When manufacturing wheels the standards sheet 6 should be followed closely, especially the coning of the thread and the fillet between the thread and the flange must be present.
3) Calculation of total rolling resistance
As mentioned before it is necessary to consider the worst situation, i. e. to add the three resistances found in section 2. To do this in a practical way, it is an advantage to use a form as that shown in fig. 8. In fig. 9, 10, 11 and 12 I have shown examples of its use as well as how different the resistance can be for the same type of wagon or carriage when constructed to different principles.
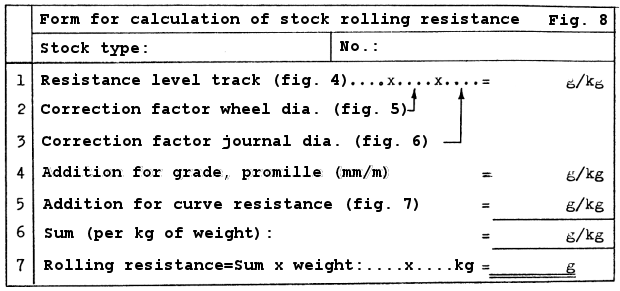
Once again I must emphasize that the results I have presented in the foregoing are average values, but that they nonetheless may give an idea of the magnitude of resistances and show how the model builder can influence the rolling resistance of a wagon during construction. This is mentioned at the end of each section as "Summary".
Click to see >> fig. 9 >> fig. 10 >> fig. 11 >> fig. 12
4) Expected pulling force
The resistance values resulting from the foregoing investigations and calculations may not themselves tell the model builder much but compared to the expected pulling force of a locomotive they become meaningful. The reason for explaining about rolling resistance first is simply that some of the explanations and calculations are of use in this section.
The maximum pulling force of a locomotive depends on at least three factors:
1) The adhesion weight of the locomotive.
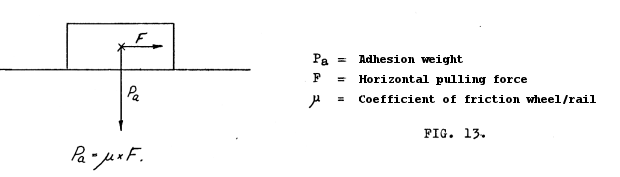
2) The coefficient of friction between the wheels and rails.
3) Resistances from non-driven wheel sets and current collectors, among others.
Re 1: The adhesion weight is the weight resting on the driven wheel sets of a locomotive. To keep this reasonably constant it is important that non-driven wheel sets, if any, are sprung such that track irregularities do not cause weight to be removed from the driven wheel sets for example if the weight is primarily resting on the non-driven wheel sets. To keep the adhesion weight as large as possible the weight resting on non-driven wheel sets should be reduced but not to less than 125 g per wheel set.
Re 2: The coefficient of friction between wheels and rails is per definition the ratio between the vertical force Pa and the horizontal force F that is needed in order to move an object with constant speed along a plane surface. This is shown in fig. 13. When the wheels and rails are reasonably clean this value is quite close to 0.2. If there is oil or similar lubricant on the rails, the value may be reduced to less than the half. The value µ = 0.2 that I will use in the following calculations is present as per the definition when the driven wheels are slipping on the rails. If slipping can be avoided the pulling force may be increased; tests show that the coefficient of friction µ0 when there is no slipping between the driven wheels and rails
![]()
When starting a heavy train it is possible to take advantage of this by starting the locomotive so carefully that slipping does not occur. One way to aid such careful starting is to build a centrifugal coupling into the drive line of the locomotive.
Re 3: Such resistances are normally rolling resistance from non-driven wheel sets and tender wheel sets calculated the same way as for wagons in the form in fig. 8, and resistances from current collectors. According to DMJK standards locomotives must be provided with two sets of current collecters of which at least one set must be in operation at any time. The downward acting force of the current collectors naturally reduce the adhesion weight of the locomotive. The force from a current collecter must according to the standards sheet 10 be between 30 g and 60 g per side. In order to keep a good electrical contact between current collectors and the third rail the force from the current collecter should be as large as possible. As a compromise I have chosen to use 60 g in the following calculations.
Before we proceed I must presuppose that the motor of the locomotive is powerful enough to bring the wheels to slip on the rails in all conditions, otherwise the calculations will be incorrect. Likewise I must presuppose that all non-driven wheel sets are suspended in such a way that they can follow the track sideways, and that they in curves are kept appr. perpendicular to the centre line of the track; i. e. that two-wheeled trucks has a pivotal point some distance from the wheel set, for instance like the Bissel truck.
In order to make the calculations in the most expedient manner I have made the form shown in fig. 14. I will add a few comments to the form refering to fig. 14 and the following forms. The form is designed such that first the pulling force available at the driven wheels is found. From this the resistances found is subtracted. In the second line are inserted two current collectors of each 60 g regardles of if both sets are mounted on the locomotive or one set is mounted on the tender. In the third line the pulling force is calculated by taking adhesion weight times coefficient of friction µ = 0.2. In the fourth line the friction force from the current collectors are subtracted as the downward force times µ = 0.2 and the number 2. In the sixth line the grade resistance for the locomotive without tender is subtracted. The other resistances are calculated in the same way as in fig. 8 as separate wagons.
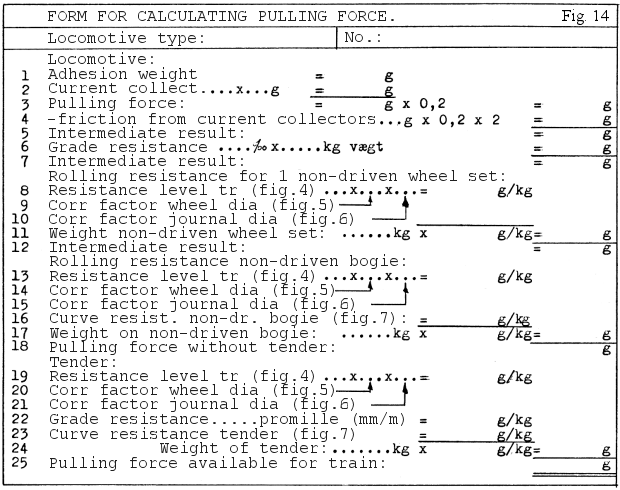
When chosing the following examples I have tried to show the use of the form with different types of locomotive as well as chosing realistic weights for the examples even though I haven't actually weighed particular models on the layout. From the examples the following guidelines may be extracted:
1) The adhesion weight should be as large as possible.
2) Non-driven wheel sets and tenders should be as light as possible.
3) As many wheel sets as possible should be driven.
4) The bearings of non-driven wheel sets should be as good as possible.
Click to see >> fig. 15 >> fig. 16 >> fig. 17 >> fig. 18 >> fig. 19
As a conclusion of this long tale I have compared the locomotives from the examples in fig. 15-19 with the rolling stock from the earlier examples in fig. 9-12 as the rolling stock is shown in the rightmost columns and the locomotives are shown in the lower rows. In the cells are written how many of the wagons or carriages in a train the locomotive in question will be able to start when the train is standing in a curve on a grade. The last column is thought to be a wagon with rolling resistance equal to the average of the preceding four.
I think that the numbers in fig. 20 look quite reasonable; but as mentioned earlier this account cannot be taken to cover all possible conditions, only that the values found by these calculation methods are not far from the truth.
| Wagons | Fig. | 9 | 10 | 11 | 12 | Average | ||
| Type | Hbis 211 5 000 | Hbis 211 5 099 | AF 78 | AF 82 | ||||
| Resistance [g] | 23 | 54 | 17 | 57 | 38 | |||
| Locomo- tives |
Fig. | Type | Pulling force [g] | Number of wagons per locomotive | ||||
| 15 | F | 118 | 5 | 2 | 7 | 2 | 3 | |
| 16 | S | 260 | 11 | 5 | 15 | 4 | 7 | |
| 17 | P | 105 | 4 | 2 | 6 | 2 | 3 | |
| 18 | My 1101 | 461 | 20 | 8 | 27 | 8 | 12 | |
| 19 | My 1108 | 107 | 4 | 2 | 6 | 2 | 3 | |
If any of the readers that have followed me this far have information that may throw further light on the subject or have any questions, please don't hesitate to contact me and I will try to answer to the best of my ability.
Changes:
2008-03-15: Translated from Danish.
2009-01-01: Typeface updated.